字符串搜索玩耍指南（二）- Boyer-Moore算法

发表于 | 分类于

本期日常：浪完了逛吃躺吃的中秋国庆小长假，我肥来了！肥归工作的第一天元气满满，决定填坑一篇～

“众里寻他千百度，蓦然回首，那人却在、灯火阑珊处。”
“那人”是不是在难说，不过今天我们要聊的字符串搜索之Boyer-Moore算法确是能借助回溯寻到“那串字符”。

来自Boyer-Moore的回眸

Boyer-Moore是Robert S. Boyer和J Strother Moore在1977年发明的算法。前文介绍的KMP是从前往后一次遍历文本（Text）进行搜索，并且采用了DFA来避免回溯操作。换个角度，若是每次使用目标字符串（Pattern）从后往前比较，我们反而能更快排除不符合的情况，及时止损，提高效率。

举个例子，如果我们要从BAAABAAABBAA中搜索BAAABB，如果从前往后比较，我们至少要进行5次比较才能在第5个字符 (嗯，你没看错，要从0开始计数哦) 发现前面的工作都白费了；而如果一开始从后往前比较，就能直接发现目标字符串的最后一个字符B与文本当前位置的A匹配失败，这个时候，我们就需要移动目标字符串。

移到哪里合适呢？分两种情况讨论：

  1. 当前文本指针指的字符不在目标字符串中：
    那么可以直接将字符串指针移动到当前文本指针的后面一个位置。
  2. 当前文本指针指的字符在目标字符串中出现：
    为了避免错过可能的匹配，则应该将目标字符串中该字符出现的最后位置与文本指针对齐。

下图以上例比较了两种操作可能造成的不同结果：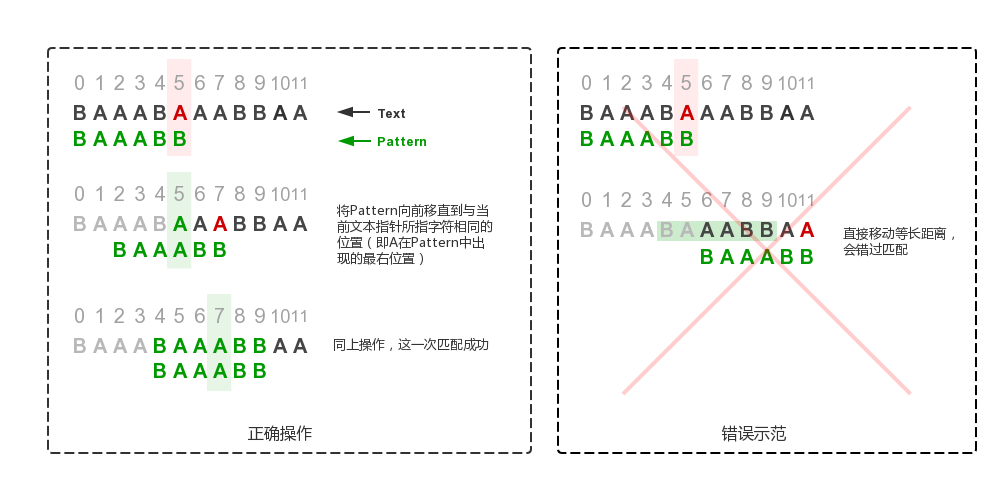
Boyermoore Example

定义移动规则

虽然Boyer-Moore算法和KMP算法的主要思路截然相反，但是在具体操作步骤中却有一定的相似性。比如，Boyer-Moore算法中最重要的一步，也是要构建一组遇到不同字符时的移动规则。
不过这个操作，相较于DFA的构建，可就简单多啦：
初始化一个right[]数组，存储给定字符集中每个字符在目标字符串中出现的最后位置，如果不在目标字符串中，则设为-1。
代码如下，非常简单：

1
2
3
4
5
6
7
8
int[] right = new int[R];
for (int c = 0; c < R; c++) {
    right[c] = -1;
}
for (int j = 0; j < M; j++) {
    // rightmost position for chars in pattern
    right[pattern.charAt(j)] = j;
}

使用规则进行字符串搜索

有了移动规则，字符串搜索就是按章办事了。
我们还是用两个指针完成搜索，i作为文本指针（text）从前往后移动，j作为长度为M的目标字符串（pattern）指针从后往前进行比较。如果遍历pattern，即j的取值为0到M，都有text.charAt(i + j)等于pattern.charAt(j)，那么匹配成功。否则，如果其中某个字符匹配失败，我们还是按两种情况处理：

  1. 匹配失败的字符不在pattern中：把pattern向前移动j + 1个位置
  2. 匹配失败的字符在pattern中：使用提前定义好的right[]数组将pattern中对应字符出现的最后位置与当前文本字符位置对齐。这一步可以通过公式i += j - right[text.charAt(i+j)]来更新i的值。
    如果j - right[c]是个小于等于0的值，也就是说这个时候重新对齐反而会把pattern往回推，这时我们需要丢弃这个值，选择直接加1，以此保证i永远是前进的。

举个例子，下面这种情况，j = 3, right[‘E’] = 5, 所以如果按照i += j - right['E']来算，i又跑回去2个字符了。遇到这种情况时，就直接i += 1就好了。

1
2
3
4
        i    i+j
. . . . . . . E L E . . . . .
        N E E D L E
              j

代码实现

下面是Boyer-Moore算法的基本实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
public class BoyerMoore {

    private int[] right;
    
    private String pattern;
    
    // pattern的长度
    private final int M;
    
    // 这里使用的Extended ASCII字符集，用于构建right[]
    private static final int R = 256;

    public BoyerMoore(String pattern) {
        this.pattern = pattern;
        M = pattern.length();
        // right[] tells how far to skip if mismatch is detected
        right = new int[R];
        for (int c = 0; c < R; c++) {
            right[c] = -1;
        }
        for (int j = 0; j < M; j++) {
            right[pattern.charAt(j)] = j; // rightmost position for chars in pattern
        }
    }
    
    public int search(String txt) {
        int n = txt.length();
        int skip;
        for (int i = 0; i <= n - M; i += skip) {
            skip = 0;
            for (int j = M - 1; j >=0; j--) {
                if (pattern.charAt(j) != txt.charAt(i + j)) {
                    // 对于不在pattern中字符，其right[c]的值为-1，
                    // 那么 i+= skip其实就跳到了i + j + 1的位置，
                    // 这样将两种情况统一处理了
                    skip = j - right[txt.charAt(i + j)];
                    if (skip < 1) skip = 1;
                    break;
                }
            }
            if (skip == 0) return i;
        }
        return n;
    }
}

进一步优化

在匹配失败发生时，对于text[i + j, i + M - 1]这部分的字符我们是已知的，即pattern[j, M - 1]部分的字符，结合KMP的思想，如果也有一个类似DFA的表，那么我们其实能更准确的移动i的位置。
完整的Boyer-Moore算法是包括了这部分优化的，这里我就没有更深入研究了，感兴趣的可以去看看原作~

对于一些典型的输入，那么Boyer-Moore算法在长度为N的文本中搜索长度为M的字符串时，只需要使用大约N/M次字符串比较就搞定了，还是非常高效的。

逐渐会发现很多算法都是从最原始的解法逐步优化，逐渐完善，博采众长或是独辟蹊径。

下一篇再介绍一个思路清奇的算法~未完待续~

参考资料

  • Algorithms, 4th Edition by Robert Sedgewick and Kevin Wayne