字符串搜索玩耍指南（一）- KMP算法

本期日常：
上午去上海WAIC溜达了一圈，惊叹于谷歌艺术计划里AI与艺术品擦出的火花。逛到Art Camera展区真的心生感激，任何藏品不可避免的自然老化过程，即使再如何减缓也无法彻底阻止，尽可能用技术高保真存留艺术品的原貌，也许是我们能为这些从古至今遗留的珍宝们做的最好的事情。

---

还是回到本篇笔记主题——字符串搜索来。
相比于艺术品欣赏这等阳春白雪，字符串搜索可谓大家日常使用最频繁的操作之一了。

稍微正式的定义一下字符串搜索：给定一串长度为N的文本（text）和一个长度为M的字符串（pattern），找到这个字符串在文本中出现的位置。

字符串搜索的几个算法都挺经典的，比如KMP，至少我在真正接触之前就久闻大名了。接下来，我们就逐个击破～

---

热身运动 Brute-Force

对于任何问题，一般都有一个最直观的最容易想到的方法。很多时候，你可能都不屑于采取暴力解决的方式，但是对于小白玩家而言，先使用原始的方法得到一些进展，之后再进一步调优/学习高阶玩法，不然很容易毫无头绪，反而乱了阵脚。脚踏实地，才是真理。（摸摸小肚子，一口吃不成胖子，肉都是日积月累长起来的啊～）

暴力解法，话不多说，直接上代码：

public class BruteForce {
    public static int search(String txt, String pattern) {
        int n = txt.length();
        int m = pattern.length();
        for (int i = 0; i <= n - m; i++) {
            for (int j = 0; j < m; j++) 
                if (text.charAt(i + j) != pattern.charAt(j))
                    break;
            if (j == m) return i; // found
        }
        return n; // not found
    }
}

不难看出，暴力解法在最差的情况下时间复杂度为O(MN)，但在绝大多数实际应用场景中，内循环的比较基本上只要进行一次，这样的话，时间复杂度近似为O(N)，要比理论最差情况好很多。

当然，在某些场景下，我们可能会遇到诸如在“AAAAAAAAB”中搜索“AAAAB”这样的字符串，针对这种情况，暴力解法就不够优秀了。

---

进阶玩法之KMP

算法的命名一般都是用其发明者的名字，KMP分别代表D.E.Knuth, J.H.Morris和V.R.Pratt三位发明者。

要了解KMP的主要思想，我们先来看看暴力解法之所以不够快的原因。
下面是暴力解法的另一种实现，更直观的表示了匹配失败后文本指针i和字符指针j的回溯。
注：这里用i表示文本指针(text pointer)，j表示字符指针(pattern pointer)。

public class BruteForce {
    public static int search(String txt, String pattern) {
        int n = txt.length();
        int m = pattern.length();
        int i, j;
        for (i = 0, j = 0; i < n && j < m; i++) {
            if (text.charAt(i) == pattern.charAt(j)) j++;
            else {
                i -= j; // explicit backup
                j = 0;
            }
        }
        if (j == m) return i - m; // found
        return n; // not found
    }
}

如下例中所示状态，在内部循环j = 3的位置进行比较时，检测到不匹配(mismatch)，因为txt[5] = 'B', pattern[3] = 'A'，所以i回退j - 1个位置，进入下一轮匹配。

0 1 2 3 4 5 6 7 8 9
A A B A A B A A B A     <= txt
      ^   ^ 
   i-j+1  i    
- - B A A A             <= pattern
          ^
          j
    0 1 2 3

其实，当我们从i - j + 1重新开始匹配时，对于这段文本中[3,5]的这部分字符，在前一轮循环中已经遍历过了，这部分的信息是已知的，我们已经知道txt[3, 5] = "AAB"，没有匹配的可能，i其实不用从i - j + 1开始，因为txt[i] = pattern[0] = ‘B'， 可以将i增 1，然后设j = 1，从 pattern 的第二个字符开始比较。

而这恰恰就是KMP算法的基本思想：利用已知的这部分信息来避免不必要的文本回溯。
通过分析几种 mismatch 的情况，我们将看到，针对每种情况，都可以利用已知信息判断该从哪儿重新开始，并且这个重置操作可以通过重置j的值来实现，而不需要回溯i, 这就保证了i永远都是前进的（正所谓开弓没有回头箭呀～）。

如何判断从哪儿重新开始呢？
这个问题的答案可以说是KMP算法的精髓所在：我们可以提前确定遇到每种情况如何重新开始，因为，这完全是由且仅由搜索的这个字符串（pattern）决定的。
稍微思考一下就能明白，当匹配失败在i处发生时，i前面的j - 1个字符就是字符串(pattern)的前j - 1个字符（否则在更早之前就应该匹配失败了～）。

---

使用DFA来表示跳转规则

现在我们知道，只要有了给定的字符串，我们就可以构建出进行匹配时，每种情况下指针的跳转规则。KMP算法引入了DFA(Deterministic finite-state automation)来表示这些规则。

举个例子来说，给定字符串ABABAC，我们可以构建如下图所示DFA：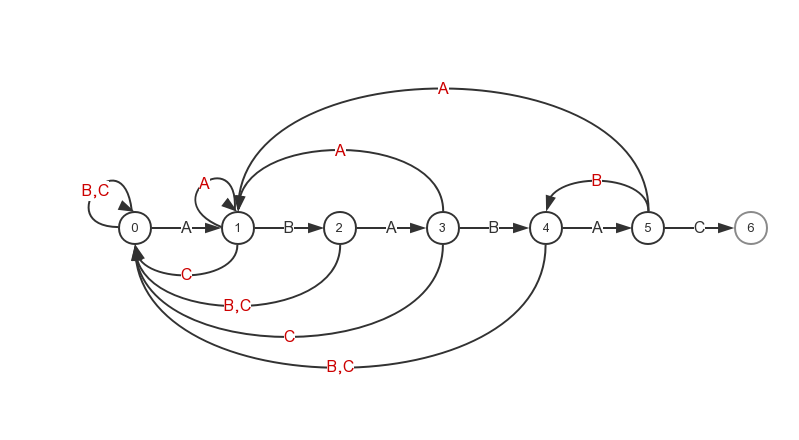

给定字符串长度为M，则DFA一共有M+1个状态，起始状态为0，结束状态为M。
上图中黑色字符前进方向的状态转换表示一次匹配成功(match)转换，红色字符反向的状态转换表示一次匹配失败(mismatch)转换。

手工画DFA很简单，怎么让代码构建出一个字符串的DFA？用什么数据结构来保存这个DFA？

如何在代码中表示DFA？

首先回答第二个问题，我们用二维数组来表示一个DFA：

// R表示字符集中所有字符的个数，这里选用Extended-ASCII字符集，所以值为256
int R = 256; 
// M表示pattern的长度，也是所有状态总数
int[][] dfa = new int[R][M];

虽然我们上图所示DFA只包含了pattern中的字符，但不表示文本中不会出现其他字符，只是在这里省略了，显而易见，在任何状态下遇到字符集里其他字符都会跳转到状态0。

对于某个字符c，dfa[c][j]就表示当我们在状态j时遇到了字符c，那么就跳转到dfa[c][j]对应的状态。

当我们进行字符串搜索时，对于文本指针i，dfa[text.charAt(i)][j]表示当我们处于状态j时遇到了字符text.chartAt(i)该跳转到的状态j'，完成跳转之后，i自增为i'，指向下一个字符，然后跳转到dfa[text.charAt(i')][j']，i自增…直到跳转到状态M(match)或者遍历完整个文本(mismatch)。

沿用上例，下面是字符串ABABAC对应的DFA数组：

char\state	0	1	2	3	4	5
pattern.charAt(j)	A	B	A	B	A	C
A	1	1	3	1	5	1
B	0	2	0	4	0	4
C	0	0	0	0	0	6

---

如何构建DFA？

现在，只剩下一步工作我们就可以使用KMP来进行字符串搜索了，也是最关键的一步，构建DFA。

字符串匹配过程中DFA的状态转移分为两种情况，在当前状态j下：

• 字符匹配成功转移
• 字符匹配失败转移

还是从简单的情况入手，不难得出，字符匹配成功时的转移很简单，就是从当前状态j转移到下一个状态j + 1，也就是dfa[pattern.charAt(j)][j] = j + 1。

那么，当我们匹配失败时，应该跳转回哪个状态呢？
上文也提到了，当我们在pattern.charAt(j)发生匹配失败时，失败前的j - 1个字符就是pattern[0, j - 1]，是已知的；而又因为匹配失败，需要向前挪一步，需要重新比较的部分就变成了pattern[1, j - 1]。因此，当我们构建在状态j时的跳转时，只需要用到之前已经构建好的从状态0到状态j-1这部分DFA的信息。所以，只要有了初始值，之后就是个动态规划问题了。

最后一个细节，重置状态的值X的如何更新。显然，X的初始值X0 = 0且在状态j时X < j；之后每一步X = dfa[patter.charAt(j)][X]。
（这一步我还想了好一会儿，大概理解了，不知道能不能解释清楚：在重置j的时候，虽然pattern.charAt(j)匹配失败了，但是前j - 1步的匹配已经让X0实现了k步转移来到了当前的X，所以对于j + 1而言，在X状态上又匹配了一次pattern.charAt(j)）

终于，我们总结一下构建DFA的几个步骤：
对于每个状态j，作如下操作：

1. 把dfa[][X]拷贝到dfa[][j]（这是在匹配失败时进行的跳转）
2. 把dfa[pattern.charAt(j)][j]设为j + 1
3. 更新X = dfa[pattern.charAt(j)][X]

---

KMP的实现

于是，在长篇大论解释了一番KMP算法的思路后，我们会看到KMP的实现代码是如此的简洁：

public class KMP {

    // Extended-ASCII字符集
    private static final int R = 256;
    // pattern的长度
    private final int M;
    // DFA
    private final int[][] dfa;

    public KMP(String pattern) {
        M = pattern.length();
        dfa = new int[R][M];
        // 初始状态X，只有匹配pattern的第一个字符成功是跳转到状态1
        // 遇到其他字符均为0
        dfa[pattern.charAt(0)][0] = 1;
        // 开始愉快地进行动态规划，设X的初始值为0
        for (int X = 0, j = 1; j < M; j++) {
            // 匹配失败，回溯到X
            for (int c = 0; c < R; c++) {
                dfa[c][j] = dfa[c][X];
            }
            // 匹配成功时，从j跳转到j+1
            dfa[pattern.charAt(j)][j] = j + 1;
            // 对于j+1而言，X应该是从最初的X走了j-1时的状态
            X = dfa[pattern.charAt(j)][X];
        }
    }

    public int search(String txt) {
        int i, j, n = txt.length();
        for (i = 0, j = 0; i < n && j < M; i++) {
            j = dfa[txt.charAt(i)][j];
        }
        if (j == M) return i - M;
        else return n;
    }
}

真的简洁！

看代码也能很清晰的得出KMP的时间复杂度在O(M + N)，M为字符串的长度，N为文本长度。

另外KMP中由于用到了字符集R，如果字符集很大，DFA的构建时间为O(MR)也是需要考虑到的。

在真实的应用场景中，如果不是经常遇到具有重复特征的文本，Brute-force的表现并不差，KMP的优化并没有太大优势。不过KMP确实证明了字符串搜索问题具有线性时间的解。

不过KMP不进行文本回溯的特点，在某些使用输入流的情况下会相对方便。否则，如果要进行文本回溯，就需要对输入流做缓存处理。

---

没想到花了半个下午加整个晚上的时间才差不过梳理了一下KMP，不过又解决了一些疑问，还是很有收获啦。（尝试看了下《算法导论》里对KMP的解释，放弃了QAQ，还是更喜欢Robert Sedgewick老爷爷的话风～

虽然KMP致力于避免文本回溯来提高性能，然而，今天根本还没来得及提起的Boyer-Moore算法反而是一个利用回溯大大提高了性能的算法，下次见。（莫名有点心疼KMP

---

参考资料

• Algorithms, 4th Edition by Robert Sedgewick and Kevin Wayne